д»ҠеӨ©з»ҷеӨ§е®¶е®үеҲ©дёҖдёӢдәҶгҖӮдёҖиҲ¬еҗҢеӯҰдјҡеҺ»жҹҗеәҰдёҠжҗңпјҢзңӢеҲ°еҗ„з§Қеҗ„ж ·зүҲжң¬зҡ„PIDзӨәдҫӢпјҢжҲ–иҖ…еҺ»GitHubдёҠзҷҪе«–гҖӮ
е…¶е®һдёҖдәӣиҠҜзүҮе…¬еҸёдјҡжҸҗдҫӣдёҖдәӣжҺ§еҲ¶йўҶеҹҹзҡ„и§ЈеҶіж–№жЎҲдәҶпјҢиҝҷйҮҢйқўе°ұдјҡеҢ…жӢ¬PIDеә“гҖӮ
жҜ”еҰӮSTзҡ„"ST Motor Control Sdk"пјҢжҲ–иҖ…TIзҡ„C2000зі»еҲ—зҡ„control suiteгҖӮ
дёҚиҝҮзӣ®еүҚTIе®ҳж–№еҜ№дәҺcontrol suiteе·Із»ҸдёҚеҶҚжҸҗдҫӣзӣёеә”зҡ„жӣҙж–°,еҸҜд»Ҙ继з»ӯдёӢиҪҪиҝҷдёӘеҘ—件.
зӣ®еүҚcontrol suiteе·Із»Ҹжӣҙж–°дёәC2000WARE-MOTORCONTROL-SDK.
йӮЈжң¬ж–Үдё»иҰҒд»Ӣз»ҚTIзҡ„control suite,иҝҷйҮҢйқўйҷӨдәҶPIDеӨ–жңүеҫҲеӨҡжҺ§еҲ¶зұ»з®—жі•пјҢ并且й…ҚзҪ®дәҶдё°еҜҢзҡ„ж–ҮжЎЈгҖӮ
еҰӮдҪ•е®үиЈ…пјҹ
иҝӣе…Ҙtiзҡ„е®ҳзҪ‘пјҢиҫ“е…Ҙcontrol suiteиҝӣиЎҢжҗңзҙўпјҢе°ұеҸҜд»ҘжүҫеҲ°зӣёеә”зҡ„е®үиЈ…еҢ…гҖӮ
иҝҷйҮҢжңүзҰ»зәҝе®үиЈ…еҢ…пјҢе’ҢеңЁзәҝе®үиЈ…еҢ…гҖӮзӣҙжҺҘеҹәдәҺеңЁзәҝе®үиЈ…еҢ…иҝӣиЎҢж“ҚдҪңеҚіеҸҜгҖӮжҲ‘们е…ҲдёӢиҪҪе®үиЈ…еҢ…гҖӮ

дёӢйқўе°ұжҳҜдёҖи·Ҝз–ҜзӢӮзӮ№еҮ»NextеҚіеҸҜпјӣ
 з•Ңйқў 1
з•Ңйқў 1 з•Ңйқў 2
з•Ңйқў 2 з•Ңйқў 3
з•Ңйқў 3 з•Ңйқў 4
з•Ңйқў 4 иҖҗеҝғзӯүеҫ…
иҖҗеҝғзӯүеҫ… е®үиЈ…жҲҗеҠҹ
е®үиЈ…жҲҗеҠҹжәҗз Ғе’Ңж–ҮжЎЈ
иҝӣе…Ҙдё»з•ҢйқўпјҢиҝҷйҮҢеҹәжң¬зҡ„дҫӢеӯҗйғҪжҳҜеҹәдәҺTIзҡ„C2000зі»еҲ—зҡ„MCUиҝӣиЎҢејҖеҸ‘зҡ„пјҢе…·дҪ“еҰӮдёӢеӣҫжүҖзӨәпјӣ
 дё»з•Ңйқў
дё»з•Ңйқўиҝӣе…Ҙдё»з•Ңйқўд№ӢеҗҺпјҢжҲ‘们еҸҜд»ҘзңӢеҲ°е·Ұдҫ§иҝҷиҫ№еҢ…еҗ«дәҶиҪҜ硬件ж–ҮжЎЈпјҢйЎ№зӣ®зӨәдҫӢиҝҳжңүзӣёеә”зҡ„ж–ҮжЎЈгҖӮ
е…¶е®һжҲ‘们иҰҒжүҫзҡ„жҳҜеҹәдәҺC2000зі»еҲ—MCUзҡ„ж•°еӯҰз®—жі•еә“пјҢеҸҜд»ҘеңЁдёӢеҲ—еҲ—иЎЁдёӯжүҫеҲ°пјӣ
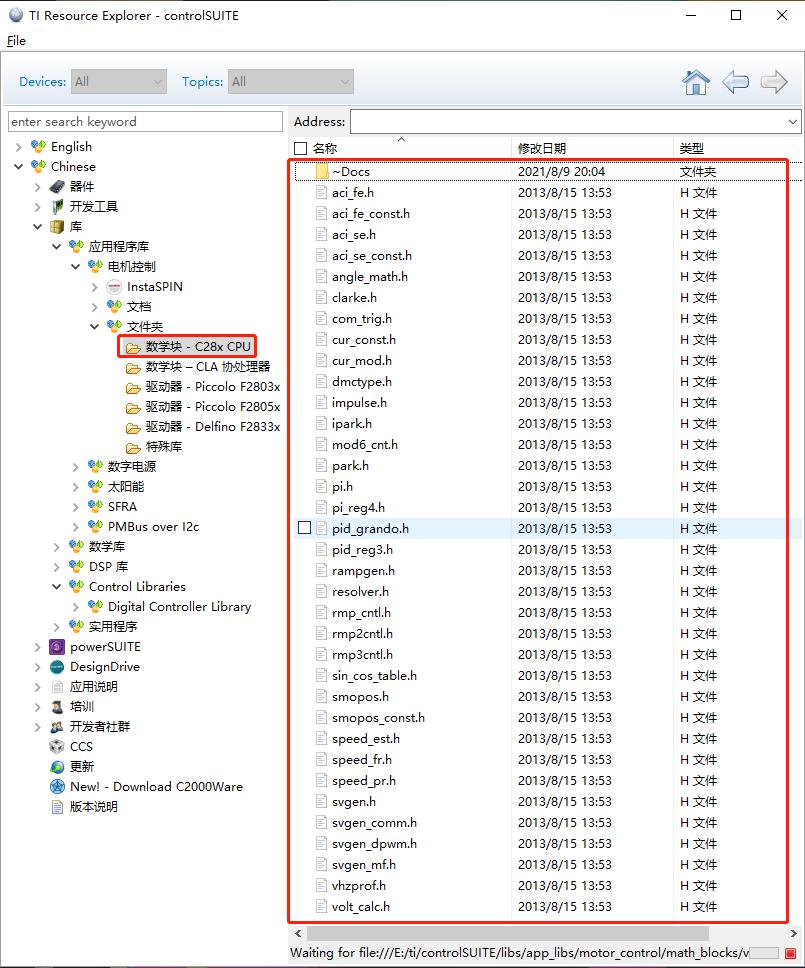
еҪ“然д№ҹеҸҜд»ҘеңЁе®үиЈ…зӣ®еҪ•C:\ti\controlSUITE\libs\app_libs\motor_control\math_blocks\v4.2дёӢйқўжүҫеҲ°зӣёеә”зҡ„PIDз®—жі•пјӣ
иҮідәҺеҰӮдҪ•дҪҝз”ЁиҝҷеҮ дёӘж–Ү件пјҢиҝҷйҮҢд№ҹжҸҗдҫӣдәҶзӣёеә”зҡ„ж–ҮжЎЈпјҢеңЁDocsдёӯжүҫеҲ°пјҢ
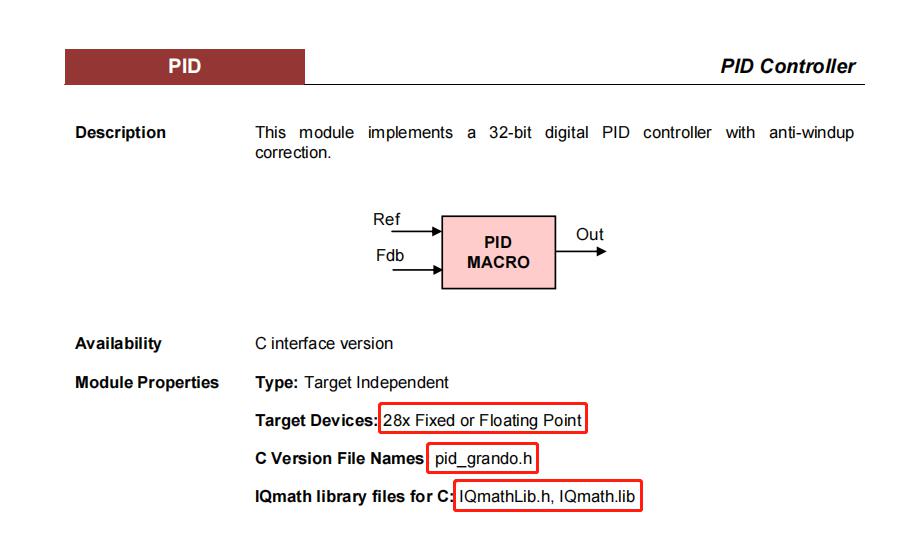
дҫӢеҰӮpid_grando.hж–Ү件пјҢиҝҷйҮҢд»Ӣз»ҚдәҶеҜ№еә”зҡ„е№іеҸ°пјҢеҪ“然жҳҜTIзі»еҲ—зҡ„MCUпјҢ并且дҫқиө–дәҺIQMathеә“пјҢе…¶е®һиҝҷйҮҢжҲ‘们еҒҡдёҖдәӣз®ҖеҚ•зҡ„ж”№еҠЁпјҢе°ұеҸҜд»Ҙ移жӨҚеҲ°иҮӘе·ұжүҖйңҖзҡ„е№іеҸ°дёҠеҺ»дәҶпјҢе…·дҪ“жәҗз ҒеҰӮдёӢпјҡ
/* =================================================================================
File name: PID_GRANDO.H
===================================================================================*/
#ifndef __PID_H__
#define __PID_H__
typedef struct { _iq Ref; // Input: reference set-point
_iq Fbk; // Input: feedback
_iq Out; // Output: controller output
_iq c1; // Internal: derivative filter coefficient 1
_iq c2; // Internal: derivative filter coefficient 2
} PID_TERMINALS;
// note: c1 & c2 placed here to keep structure size under 8 words
typedef struct { _iq Kr; // Parameter: reference set-point weighting
_iq Kp; // Parameter: proportional loop gain
_iq Ki; // Parameter: integral gain
_iq Kd; // Parameter: derivative gain
_iq Km; // Parameter: derivative weighting
_iq Umax; // Parameter: upper saturation limit
_iq Umin; // Parameter: lower saturation limit
} PID_PARAMETERS;
typedef struct { _iq up; // Data: proportional term
_iq ui; // Data: integral term
_iq ud; // Data: derivative term
_iq v1; // Data: pre-saturated controller output
_iq i1; // Data: integrator storage: ui(k-1)
_iq d1; // Data: differentiator storage: ud(k-1)
_iq d2; // Data: differentiator storage: d2(k-1)
_iq w1; // Data: saturation record: [u(k-1) - v(k-1)]
} PID_DATA;
typedef struct { PID_TERMINALS term;
PID_PARAMETERS param;
PID_DATA data;
} PID_CONTROLLER;
/*-----------------------------------------------------------------------------
Default initalisation values for the PID objects
-----------------------------------------------------------------------------*/
#define PID_TERM_DEFAULTS { \
0, \
0, \
0, \
0, \
0 \
}
#define PID_PARAM_DEFAULTS { \
_IQ(1.0), \
_IQ(1.0), \
_IQ(0.0), \
_IQ(0.0), \
_IQ(1.0), \
_IQ(1.0), \
_IQ(-1.0) \
}
#define PID_DATA_DEFAULTS { \
_IQ(0.0), \
_IQ(0.0), \
_IQ(0.0), \
_IQ(0.0), \
_IQ(0.0), \
_IQ(0.0), \
_IQ(0.0), \
_IQ(1.0) \
}
/*------------------------------------------------------------------------------
PID Macro Definition
------------------------------------------------------------------------------*/
#define PID_MACRO(v) \
\
/* proportional term */ \
v.data.up = _IQmpy(v.param.Kr, v.term.Ref) - v.term.Fbk; \
\
/* integral term */ \
v.data.ui = _IQmpy(v.param.Ki, _IQmpy(v.data.w1, (v.term.Ref - v.term.Fbk))) + v.data.i1; \
v.data.i1 = v.data.ui; \
\
/* derivative term */ \
v.data.d2 = _IQmpy(v.param.Kd, _IQmpy(v.term.c1, (_IQmpy(v.term.Ref, v.param.Km) - v.term.Fbk))) - v.data.d2; \
v.data.ud = v.data.d2 + v.data.d1; \
v.data.d1 = _IQmpy(v.data.ud, v.term.c2); \
\
/* control output */ \
v.data.v1 = _IQmpy(v.param.Kp, (v.data.up + v.data.ui + v.data.ud)); \
v.term.Out= _IQsat(v.data.v1, v.param.Umax, v.param.Umin); \
v.data.w1 = (v.term.Out == v.data.v1) ? _IQ(1.0) : _IQ(0.0); \
#endif // __PID_H__
иҝҷйҮҢйқўдёҚд»…д»…еҒҡдәҶз§ҜеҲҶжҠ—йҘұе’ҢпјҢиҝҳжңүеҜ№еҫ®еҲҶзҺҜиҠӮзҡ„ж»ӨжіўеӨ„зҗҶпјҢжүҖд»Ҙеә”з”ЁеҲ°йЎ№зӣ®дёӯжҳҜжІЎжңүй—®йўҳзҡ„гҖӮ
д»Јз ҒдёӯйңҖиҰҒдәҶи§ЈQж јејҸзҡ„зӣёе…ізҡ„зҹҘиҜҶпјҢеҸҜд»ҘеҸӮиҖғдёҖдёӢжҲ‘зҡ„иҝҷзҜҮж–Үз« пјӣ
еҸҰеӨ–пјҢиҝҷдёӘи·Ҝеҫ„дёӢзҡ„ж–ҮжЎЈдёӯпјҢиҝҳжҸҗдҫӣдәҶзӣёеә”зҡ„ExampleпјҢд»ҘеҸҠPIDзҡ„дҝЎеҸ·жөҒеӣҫпјҢе…·дҪ“еҰӮдёӢжүҖзӨәпјҡ

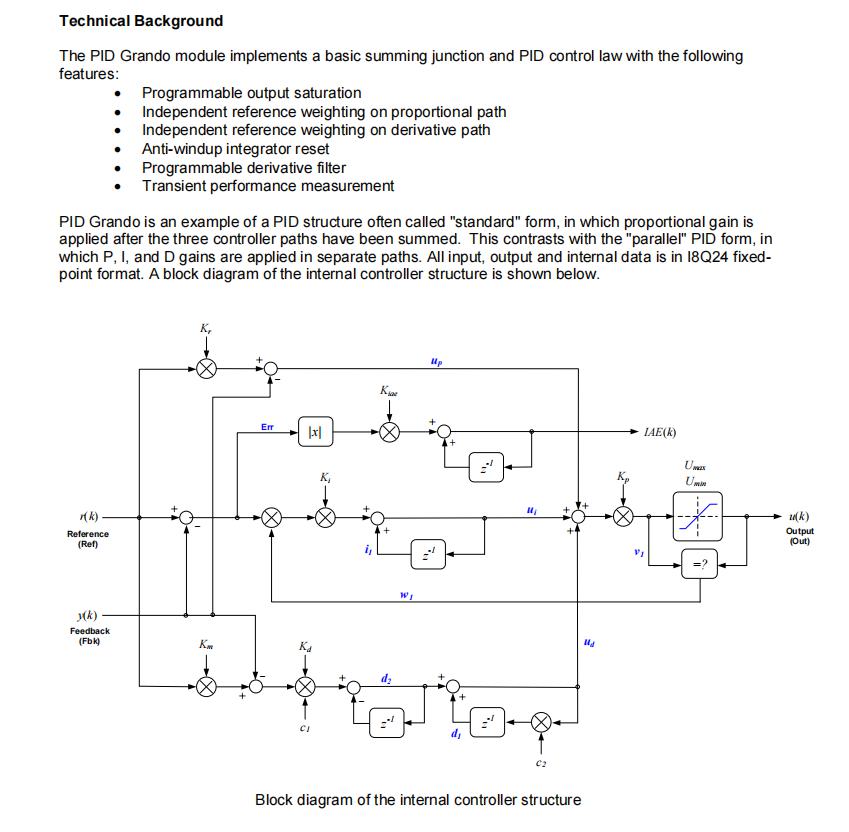
жүҖд»ҘпјҢж•ҙдҪ“жқҘиҜҙпјҢиҝҷдёӘйғЁеҲҶзҡ„жәҗз Ғд»ҘеҸҠиө„ж–ҷйғҪйқһеёёжңүеҸӮиҖғд»·еҖјпјҢз”ұдәҺзҰ»зәҝж–Ү件еӨӘеӨ§пјҢеҗҺеҸ°еӣһеӨҚгҖҗ618гҖ‘иҺ·еҸ–зӣёеә”е®үиЈ…ж–Ү件гҖӮ


????зӮ№еҮ»е…іжіЁпјҢжҠҖжңҜе№Іиҙ§еҮҶж—¶йҖҒиҫҫпјҒ????


